Глава 8. НЕКОТОРЫЕ ЭКСПЕРИМЕНТЫ

Глава 8. НЕКОТОРЫЕ ЭКСПЕРИМЕНТЫ

8.6. УМОЗРИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ С ИНТЕЛЛЕКТУАЛЬНОЙ ЗАДАЧЕЙ

Представляется очень заманчивым, вполне возможным и не очень сложным при минимальном организационном обеспечении работы заставить модель автомата решить некоторые явно интеллектуальные задачи. Хотелось бы продемонстрировать решение частной шахматной задачи: поставить мат "голому" королю королем и ладьей, когда автомат самостоятельно и не по образцу должен найти идею построения такого мата и в автомате должны образовываться конструкции памяти, реализующие в общем виде алгоритм построения такого мата, т.е. построение мата из любых начальных условий. Вторая очень заманчивая задача — открыть закон натурального ряда по нескольким его проявлениям. Читатель, которого идеи индуктивного автомата смогли заинтересовать в достаточной мере, мог бы попробовать решить эти задачи (как и другие, которые ему могут понравиться). Задачу "открой закон" мы сейчас рассмотрим в умозрительном эксперименте, рассмотрим схему решения некоторой конкретной задачи с целью показать, как вполне интеллектуальная задача приводится к чисто механическим задачам упорядочения среды.

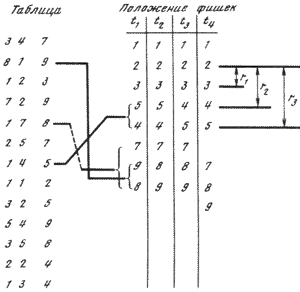
Рис.8.8. К интеллектуальной задаче

Задача состоит в следующем. Автомату предлагается ситуация — таблица из примеров на сложение (слева на рис. 8.8). Цифры для автомата — это всего лишь зрительно знакомые символы. В распоряжении автомата имеются маркированные цифрами фишки, которые он по своему желанию может переставлять в правой части зрительного поля. Требуется, чтобы автомат по собственному желанию построил из фишек отрезок натурального ряда: 1,2,3,...,9. Для усиления задачи и в таблице примеров, и среди фишек нет цифры 6. Построив натуральный ряд, автомат должен для этой цифры оставить место, должен предположить, что в природе имеется, пока не известный ему, объект с определенными свойствами.

Работа автомата состоит в том, что он выбирает из ситуации-таблицы некоторые подситуации, наиболее устойчивые для восприятия, такие, на которых можно "задержаться подольше". В силу утомляемости работающих ЭП подситуации сменяются. Новые подситуации учитывают изменения в памяти от старых, наблюдавшихся им ранее, подситуаций.

Итак, вот какими представляются основные фазы в решении задачи о понимании свойств чисел.

8.6.1. Обнаружение различной повторяемости у разных цифр. Автомат "обращает внимание" на ту часть ситуации, где объекты расположены плотнее, и выделяет те объекты, которые повторяются чаще. Для того чтобы помочь автомату в этом, расстояния между слагаемыми сделаны меньшими, чем до суммы, — автомат выделяет столбцы слагаемых и из них выбирает 1 или 2 как наиболее часто встречающиеся объекты, быстрее обращает на них внимание. Когда ЭП считываемого объекта устанет, автомат перейдет на, как правило, следующий по встречаемости объект и т.д. Результатом этого процесса — первой фазы решения задачи — будет то, что статистика встречаемости цифр-слагаемых найдет отражение в ЭП-"цифрах". Для ЭП-"цифр", чаще встречающихся, внутренние связи будут больше, чем для маловстречавшихся. На первой фазе автомат просто решает "базовую задачу", выделяя из общей ситуации, из двух столбцов слагаемых, простейшие подситуации из одинаковых цифр. Подситуации различаются по числу цифр, в них входящих. В "сильных" подситуациях цифр больше.

8.6.2. Автомат "играет в кубики". Автомат выстраивает из кубиков ряд, примерно соответствующий распределению встречаемости цифр. Помощь автомату в этом месте задачи состоит в том, чтобы временно "закрыть" таблицу. Игра в кубики выражает стремление автомата привести среду в порядок по "яркостям" объектов, по их встречаемости, обнаруженной на первой фазе.

8.6.3. Автомат обнаруживает корреляцию. Автомат обнаруживает корреляцию между таблицей и рядом. Когда в зрительном поле есть таблица и ряд, автомат выделяет устойчивые подситуации, в которые входят элементы и таблицы и ряда. На рис. 8.8 элементы подситуации связаны линиями. Устойчивость этих подситуаций обусловлена тем, что в них входят по две цифры в двух разных местах, а это дает возможность "отдыхать" и рецепторам и ЭП, а значит, автомат на таких подситуациях может задерживать внимание дольше, чем на других. В устойчивых подситуациях этого типа есть общее: цифра 1 в примере и соседство элементов в ряде. Это общее закрепляется в памяти, образуются связи ЭП1« ЭПr1. После того как эти связи образовались, ведущим элементом процесса считывания делается наличие 1 в примере. Автомат ищет 1, "зная", что если есть 1, будет устойчивая подситуация. ЭП1 становится ОВ, и это заставляет автомат отбирать соответствующие подситуации.

8.6.4. Автомат обнаруживает противоречия и исправляет ряд. В таблице для примера (17 8) расстояние между 7 и 8 ряда не единица, что при восприятии вызовет неустойчивость считывания, рост дефицита питания ЭЦ, раздражение и действие: перестановку объектов 8 и 9 местами. С точки зрения расположения кубиков "по яркости" такая перестановка законна.

8.6.5. Автомат фиксирует в памяти дальнейшие "утверждения": ЭП2« ЭПr2; ЭП3« ЭПr3 и т.д. После того как устанут ЭП1 и ЭПr1, автомат найдет устойчивые подситуации на базе 2, 3 и т.д.

8.6.6. Автомат "делает нетривиальное утверждение". Автомат выдвигает гипотезу о существовании и свойствах объекта, не представленного в ситуации. В таблице отсутствует цифра 6, что некоторые "законные" подситуации делает неверными, вызывающими "неудовольствия". Например, комбинация 25 7 требует, чтобы в ряду между 5 и 7 расстояние было r₂, а не r₁). Избавляясь от этого противоречия, автомат раздвигает ряд и оставляет место для 6.

Для интеллектуальной задачи будет интересным сделать так, чтобы автомату было полезно пользоваться таблицей: решать какие-то другие задачи с ее помощью. Например, можно ввести в среду некоторый "арифмометр", с помощью которого автомат может из одних объектов получать другие, которые ему требуются, используя ограниченный и меняющийся набор объектов, имеющихся во внешней среде. В этом случае знания о свойствах объектов становятся нужными автомату и переход от таблицы к ряду существенно упрощает и расширяет его возможности и знания.

8.6.7. Образование доминанты. Последнее об интеллектуальной задаче. Раздвинув ряд и сделав все ситуации-примеры законными и согласующимися с расстояниями между цифрами в ряду, автомат испортил ряд. Ряд стал теперь с "дыркой". Ряд с дыркой — это нарушение требования порядка, неустойчивость восприятия, эмоциональная травма. В автомате формируется устойчивая доминанта — "заноза в мозгу", "пунктик": заполнить дырку. Автомат теперь знает, что в мире должен быть объект с уже известными автомату свойствами, присущими цифре 6. У автомата появилась "цель жизни": найти (или создать, если есть "арифмометр") объект с требуемыми свойствами. Каждый зрительно новый дня него объект автомат будет теперь проверять: а нельзя ли заполнить им свободное место в ряду и снять постоянный источник раздражения. "Пунктик" материализуется в виде образования сильного потенциального очага возбуждения из элемента памяти ЭПr₆ — элемента пространственной памяти для клетки, в которой должна быть шестерка. Место может быть не обязательно "жестким", а определяться положением "дырки" в ряду.